¿cómo determino el rango, la moda, media y mediana en la siguiente muestra?
23- 25- 28- 23- 35- 32- 27- 30- 31- 31
Rango = (Dato mayor) - (Dato menor) = 35 - 23 = 12
Moda = Dato que aparece más veces = 23, 31 (puede haber más de una)
Media = Se suman todos y se dividen entre el número de ellos = (23 + 25 + 28 + 23 + 35 + 32 + 27 + 30 + 31 + 31) / 10 = 285 / 10 = 28.5
viernes, 18 de junio de 2010
domingo, 13 de junio de 2010
Poliedros regulares
Desarrollo del Tetraedro
Desarrollo del cubo
Desarrollo del octaedro
Desarrollo del dodecaedro
Desarrollo del icosaedro
Desarrollo del prisma
Desarrollo del ortoedro
Desarrollo de la pirámide
Desarrollo del tronco de pirámide
Desarrollo del cilindro
Desarrollo del cono
Desarrollo del tronco de cono
lunes, 7 de junio de 2010
miércoles, 2 de junio de 2010
Pirámide
En la figura se indican los elementos más notables de una pirámide.
Las pirámides se puede clasificar de forma análoga a los prismas. Así, hay pirámides rectas y oblicuas, según que el centro del polígono de la base coincida o no con el pie de la altura de la pirámide, y regulares eirregulares, según que el polígono de la base sea o no regular. Así mismo, según el número de lados del polígono de la base, la pirámide será triangular, cuadrangular, pentagonal, etc.
ÁREAS LATERAL Y TOTAL DE UNA PIRÁMIDE
Con cartulina, construye una pirámide pentagonal, como la de la figura, y córtala según se indica.
¿Cuál será el área lateral y total de la pirámide de la figura?
En las pirámides rectas y de base regular, las caras laterales serán triángulos isósceles todos iguales. El área lateral de la pirámide será, por tanto, la suma de las áreas de estos triángulos, es decir:
donde P es el perímetro de la base y a la apotema de la pirámide.
El área total será 
donde a’ es la apotema del polígono de la base.
TRONCO DE PIRÁMIDE
Si cortamos una pirámide por un plano, obtenemos un tronco de pirámide, que será recto u oblicuo, según que el plano sea o no paralelo a la base.
Fíjate en que las caras laterales de un tronco de pirámide son trapecios y cuando éste es regular, entonces los trapecios son isósceles iguales y su altura coincide con la apotema del tronco de pirámide. Por otra parte, las bases son polígonos semejantes.
El área lateral del tronco de pirámide regular será la mitad del producto de su apotema por la suma de los perímetros de las bases, es decir, 
.
El área total será la suma del área lateral y el área de las dos bases.
viernes, 28 de mayo de 2010
La circunferencia y el círculo
Actividad: LONGITUD DE LA CIRCUNFERENCIA pincha AQUÍ
La circunferencia es una línea curva cerrada, cuyos puntos tienen la propiedad de equidistar de otro punto llamado centro. El término equidistar significa que están a la misma distancia. Los puntos de la circunferencia y los que se encuentran dentro de ella forman una superficie llamada círculo.
Principales elementos de la circunferencia.- A continuación le explicamos las partes que conforman una circunferencia.
-Radio: es el segmento que une el punto centro con cualquier punto de la circunferencia. El radio permite nombrar a la circunferencia y lo identificamos con la letra r.
-Diámetro: segmento que une dos puntos de la circunferencia, pasando por el punto centro. El diámetro equivale a la medida de dos radios.
-Cuerda: es un trazo que une dos puntos de la circunferencia.
-Arco: es una parte o subconjunto de la circunferencia, limitada por dos puntos de ella.
Cómo calcular la longitud de una circunferencia.- Los matemáticos griegos decidieron indicar, con una letra de su alfabeto, el número de veces que la circunferencia contiene su propio diámetro. La letra escogida fue la letra π. Del número π, se conocen muchas cifras (tiene infinitas). Como las primeras son 3,141592653589...pero normalmente consideramos como valor de π 3,14.
Fórmula: Longitud de la circunferencia = π . diámetro L= D x π
El área del círculo se calcula de la siguiente forma:
A (círculo) = π · r2
Pincha AQUÍ para hacer actividades interactivas
viernes, 14 de mayo de 2010
domingo, 9 de mayo de 2010
Áreas
TRIÁNGULO
El triángulo es un polígono formado por tres lados y tres ángulos.
La suma de todos sus ángulos siempre es 180 grados.
Para calcular el área se emplea la siguiente fórmula:
Área del triángulo = (base . altura) / 2
CUADRADO
El cuadrado es un polígono de cuatro lados, con la particularidad de que todos ellos son iguales. Además sus cuatro ángulos son de 90 grados cada uno.
El área de esta figura se calcula mediante la fórmula:
Área del cuadrado = lado al cuadrado
RECTÁNGULO
El rectángulo es un polígono de cuatro lados, iguales dos a dos. Sus cuatro ángulos son de 90 grados cada uno.
El área de esta figura se calcula mediante la fórmula:
Área del rectángulo = base.altura
ROMBO
El rombo es un polígono de cuatro lados iguales, pero sus cuatro ángulos son distintos de 90ª.
El área de esta figura se calcula mediante la fórmula:
Área del rombo = (diagonal mayor.diagonal menor) / 2
TRAPECIO
El trapecio es un polígono de cuatro lados, pero sus cuatro ángulos son distintos de 90º.
El área de esta figura se calcula mediante la fórmula:
Área del trapecio = [(base mayor + base menor).altura] / 2
PARALELOGRAMO
El paralelogramo es un polígono de cuatro lados paralelos dos a dos.
El área de esta figura se calcula mediante la fórmula:
Área del paralelogramo = base.altura
PENTÁGONO
El pentágono regular es un polígono de cinco lados iguales y cinco ángulos iguales
El área de esta figura se calcula mediante la fórmula:
Área del pentágono = (perímetro.apotema) / 2
HEXÁGONO
El hexágono regular es un polígono de seis lados iguales y seis ángulos iguales.
Los triángulos formados, al unir el centro con todos los vértices, son equiláteros.
El área de esta figura se calcula mediante la fórmula:
Área del hexágono = (perímetro.apotema) / 2
CÍRCULO
El círculo es la región delimitada por una circunferencia, siendo ésta el lugar geométrico de los puntos que equidistan del centro.
El área de esta figura se calcula mediante la fórmula:
Área del círculo = 3'14.radio al cuadrado
sábado, 1 de mayo de 2010
martes, 13 de abril de 2010
Diviértete y aprende
En este enlace encontrarás test variados de Matemáticas ; anímate y entra. En la página te divertirás, aplicarás tus conocimientos y aprenderás " muuuuchas" matemáticas.
domingo, 11 de abril de 2010
Repaso de geometría
Ángulo obtuso: un ángulo obtuso tiene una abertura mayor a la del ángulo recto, concretamente 180º.
Ángulo agudo: un ángulo agudo tiene una abertura menor a la del ángulo recto.
Ángulo plano: es aquel cuyos lados son semirrectas opuestas, además el ángulo es la mitad de una revolución, o sea, 180º.
Ángulo completo: un ángulo completo equivale a 360º
Los ángulos complementarios son aquellos cuya suma de medidas es 90º
Dos ángulos suplementarios son aquellos cuya suma de medidas es 180º
Dos ángulos opuestos por el vértice son los ángulos opuestos cuando se cruzan dos líneas
Dos ángulos son Consecuticos si tienen un lado común y un vértice común.
Dos ángulos son Adyacentes si tienen un lado común, un vértice común y los lados no comunes están en la misma recta.
Pincha AQUÍ y tendrás recursos y actividades para repasar el tema
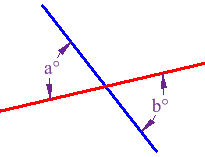
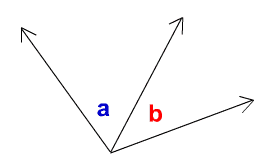
Porcentaje
Si pinchas AQUÍ podrás aprender qué es un porcentaje, formas para calcularlo y un taller para que practiques los tantos por cientos.
jueves, 8 de abril de 2010
Tanto por ciento o porcentaje
La palabra "por ciento" significa "por cien", como si dividieras algo por cien. En otras palabrabs, por ciento significa una centísima parte de algo. Un por ciento es 1/100, 67% es 67/100, etcétera.
Consideramos alguna cantidad, por ejemplo 65 o 489€ o 1.392, como "un total". Si divides este "total" a cien partes iguales en su mente, entonces cada parte es un por ciento del total.
Cómo hallar un porcentaje o tanto por ciento de un número
Para hallar 24% o 8% o cualquier otro porcentaje de alguna cantidad, puedes primero hallar el 1% de la cantidad, y luego multiplicar el resultado por 24 o 8 o cualquier sea su tanto por ciento.
Ejercicio: cálculo de tantos por ciento
1. ¿Cuál es el 25 % de 480?
Resolución:
En este caso A = 480 y t = 25. Se debe calcular B.
El 25% de 480 es 120.
2. Calcular qué tanto por ciento de 320 es 80.
Resolución:
Obsérvese que en este caso A = 320, B = 80 y se ha de calcular t.
3. El 15 % de cierta cantidad es 54. Calcular esa cantidad.
Resolución:
t = 15 B = 54
4. En una clase de 30 alumnos, 8 practican la natación y 22 juegan al fútbol. Hallar el porcentaje de alumnos que practica cada deporte.
Resolución:
El 26,6 % de los alumnos practica la natación.
El 73,3 % de los alumnos juega al fútbol.
lunes, 22 de marzo de 2010
Operaciones con fracciones
Suma y resta de fracciones
Con distinto denominador
1. Se reducen los denominadores a común denominador:
1º Se determina el denominador común, que será el mínimo común
múltiplo de los denominadores.
2º Este denominador, común, se divide por cada uno de los denominadores,
multiplicándose el cociente obtenido por el numerador correspondiente.
2. Se suman o se restan los numeradores de las fracciones
equivalentes obtenidas.
m.c.m.(4, 6) = 12
Multiplicación de fracciones
El producto de dos fracciones es otra fracción que tiene:
Por numerador el producto de los numeradores.
Por denominador el producto de los denominadores.
División de fracciones
El cociente de dos fracciones es otra fracción que tiene:
Por numerador el producto de los extremos.
Por denominador el producto de los medios.
Suscribirse a:
Entradas (Atom)
